商业分析微观案例#3:蒙特卡罗模拟的更好决策
Background
最近的一次 路透 文章讨论了美国零售商是如何采购的, 然后储存, 这些商品预计将对中国进口商品征收25%的关税. 这反过来又推高了运输和储存成本 “给零售商的季度业绩增加压力”.
在我们的3rd 分析Micro-Case, 我们设身处地为零售商着想,问问自己是否能期望获得足够的增量利润,以证明加快(关税前的)采购是合理的, 给定四个主要未知数:
- 关税金额虽然预计是25%, 有可能宣布一项协议,但不征收关税, 或者最终的结果可能完全不同.
- 预期零售价格上涨我们知道25%的关税将适用于我们的采购价格.e. 我们的主营业务), 但我们也知道,i)不同的零售商有不同的COGS,关税将适用于ii)这些零售商中的一些可能愿意吸收一些关税,而不是将其转嫁给客户iii)一些制造商可能愿意吸收一些关税,以保持对当地(美国)制造商的市场份额,从而抑制一些价格上涨.
- 存储成本增加如果我们有所怀疑,我们就不是唯一一家增加库存水平的零售商, 我们还应该预料到存储成本会增加一些不确定的数量.
- 贮存期限25%的关税原定于1月1日生效, 2019, 但随后被推迟到3月2日, 2019. 因此, 目前尚不清楚货物需要储存多长时间才能实现免关税优势.
为简单起见, 我们忽略了运费的上涨, 资本成本和其他可能包含在更全面的模型中的项目.
即使只有4个未知数, 这是一个很难得出定量答案的问题. 在这个微观案例中,我们对比了传统方法(我们的决策模型基于平均估计)。, 使用蒙特卡罗(MC)模拟方法(我们根据各自的概率模拟所有潜在结果). 因此,我们展示了MC模拟如何防止决策过程中毫无根据的乐观主义.
是基线
为了模拟这个, 假设我们的关税前价格是100美元, 相应的40%销货成本(需缴纳关税). 同时假设,存储成本在基准模型中每单位/月增加1美元的成本.
因此,我们的关税前利润是59美元.
这个基本的余量公式在以后的所有计算中使用, 然而,相关价格, 销货成本和库存根据我们的型号规格进行调整.
现在,假设我们已经进行了适当的研究,并得出如下结论:
- 关税最有可能以25%的税率实施
- 零售价格平均上涨10%.
- 存储成本将增加20%.
- 库存平均为4个月.
因此,在没有任何库存积累的情况下,我们的预期关税后利润率预计为59美元。
在我们的简化示例中, 预期的价格上涨正好抵消了关税的影响,利润率保持不变. 我们是否增加库存的决定取决于我们是否相信我们将获得高于59美元基准利润率的利润率.
传统的(单点估计)方法
用传统方法计算我们的预期收益, 我们使用价格和存储成本的平均预期增长, 再加上预计四个月的存储成本. )关税可以忽略不计,因为我们是在关税生效前进口货物的.),可计算为:
似乎按照我们的平均计算方法,我们期望赚65美元.每件产品的利润率是20美元,而我们的基准是6美元.比我们的预期利润多出了20美元,而没有进行储备工作. 这听起来令人印象深刻,这是一个健康的6.比没有储备的情况下预期的利润率高出2%.
然而, 这种方法不能识别每个变量固有的风险或可变性, 因此产生了一个相对不知情的结果.
蒙特卡罗模拟方法
蒙特卡罗模拟 是否有一类广泛的计算算法依赖于重复的随机抽样来获得数值结果 (维基百科). 具体地说, 我们的MC模型从4个未知变量中随机选择一个值,每个值与该变量的指定概率一致, 并计算相应的改进边际为该组合的投入. 我们这样做10万次来生成改进后的边际的概率分布.
输入分布
我们对上述4个未知数中的每一个都增加了研究结论, 其概率分布保持平均值,如前所述. 定义概率分布需要一定程度的专业知识来应用于该分布, 我们假设已经在下面应用了:
关税分布
关税金额:我们认为,25%的关税有80%的可能性得到实施,20%的可能性达成协议,维持现有的0%关税. 用数字来表示, 我们从集合{0%中抽取样本(进行替换), 25%},每幅画的概率为20%, 80%}.
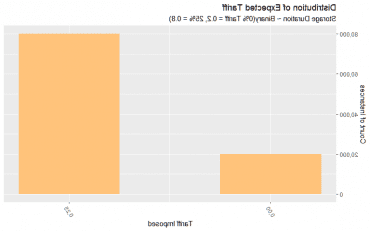
价格上涨
预期价格上涨25%的关税只适用于我们的销货成本,占我们价格的40%. 因此, 如果我们想把关税完全转嫁给我们的客户, 我们的价格需要提高10%.4 * .25). 我们假设一个正态分布,平均增长10%,标准差为4%. 因此, 我们有95%的信心,我们的实际价格涨幅将大约在2%-18%(10% +- 1)之间.96 * 4%).
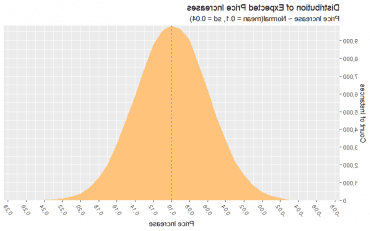
存储成本
存储成本增加在这里,我们假设一个正态分布,均值为20%,标准差为5%(因此存储增量的95% CI为10%-30%)。.

贮存期限
贮存期限:免关税购买所需的持续时间(以月为单位). 在这里,我们使用泊松分布,因为我们希望持续时间以零为界,并且持续时间大的概率很小. 我们使用4个月的平均值.
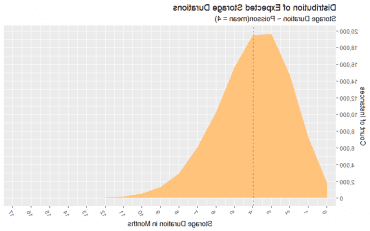
计算可能差额
根据假设和概率分布, 我们从4个输入变量中随机选择一个,然后计算相关的改进裕度, 100,000倍. 我们现在计算每一级利润率提高的实例.
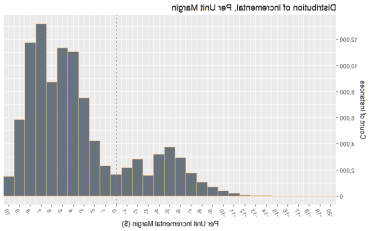
基于这种方法,我们可以预期每单位的平均增量利润为3美元.42, 95%置信区间为-7美元.5 to $9.097. 这是一个相当大的合理的边际范围,我们的结果是预期的,它应该被视为一个相当冒险的主张.
每单位增量利润率的中位数是5美元.058.
这意味着增量利润为3美元.42美元比6美元便宜多了.使用单点估计方法并结合可能的保证金变化范围(~ 16美元),预计将增加20美元.60美元对0美元),这是一项比之前理解的风险要大得多的事业. 这在很大程度上是由于我们考虑到(20%)根本不征收关税的可能性, 但一个没有考虑到这种结果可能性的模型肯定是不够的.
防范毫无根据的乐观
使用平均值来确定预期输出值并没有考虑可能值的范围,因此在做出此类决定时没有考虑所涉及的风险. 通过MC模拟, 我们不仅被迫考虑可能输入值的范围, 但是我们的输出变量的信息量要丰富得多, 哪个会让你做出更明智的决定.
使用平均值来确定结果往往过于乐观,因为模型很少考虑负面事件所产生的不成比例的高影响. 在我们的例子中, 与基准相比,不征收关税将对利润率的改善产生负面影响——约占我们模拟的20% , 低于平均价格和高于平均存储时间的组合-约占我们模拟的18%. 这两个微妙之处在单点估计中都丢失了,但幸运的是, 通过MC模拟,我们可以防止这种毫无根据和无意的乐观.